



Anhang: eine kurze Einfuehrung ueber Differentialgeometrie, den realen Gauss und die Taetigkeit des Geometers
1. Kurven:
Ich gehe hier vom dreidimensionalen Anschaungsraum aus. Eine Verallgemeinerung auf hoeherdimensionale Raeume ist nicht schwierig. Eine Raumkurve ist eine Funktion p(t), wobei jedes p(t) ein Punkt im Raum ist, also durch seine kartesischen Koordinaten x(t), y(t) und z(t) beschrieben werden kann. Die Bogenlaenge einer Kurve wird durch das Mass (die "Metrik") |p'(t)| bestimmt, d.h. sie ist gegeben durch das Integral |p'(t)|dt zwischen Anfangs- und Endpunkt.
Die Kruemmung der Kurve im Punkte t hat die Richtung von p''(t) und ist gegeben durch k(t)=|p'(t) x p''(t)|/|p'(t)|**3 (x ist das Vektorprodukt). Man kann das Inverse 1/k(t) als Kruemmungsradius desjenigen Kreises interpretieren, der sich im Punkte p(t) an die Kurve anschmiegt. In "natuerlicher Parameterdarstellung" p(s) mit s=Integral|p'(t)|dt gilt: k(t)=|p''(t)|.
2. Flaechen:
Flaechen sind Funktionen der Form f(t1,t2), die im dreidimensionalen Raum aus drei kartesischen Funktionen x(t1,t2), y(t1,t2) und z(t1,t2) bestehen. Die beiden Parameter t1 und t2 lassen sich als Koordinaten einer gedachten Ebene auffassen. Falls die Flaeche genuegend glatt (d.h. ohne singulaere Punkte) ist, kann man an jedem Raumpunkt p(t1,t2) eine Tangentialebene definieren, die ein Spezialfall fuer eine solche gedachte Ebene ist. Die Metrik auf der Flaeche wird durch die sogenannte erste Fundamentalform festgelegt ds**2=g11*du**2+2*g12*du*dv+g22*dv**2, wobei gij das Skalarprodukt der ersten Ableitungen von p nach ti bzw tj sind, also gij(t1,t2)=dp/dti.dp/dtj und der Punkt fuer das Skalarprodukt steht.
Flaechenkurven sind Kurven, die ganz in der Flaeche verlaufen. Ihre Laenge wird durch die erste Fundamentalform bestimmt; sie ist naemlich durch das Integral s=Integral wur(g11*t1'(t)**2 +2*g12*t1'(t)*t2'(t) +g22*t2'(t)**2)dt gegeben, wobei wur die Quadratwurzel bezeichnet.
Es sei eine Flaechenkurve in "natuerlicher Parameterdarstellung" p(s) (statt p(t)) gegeben (siehe oben). Der Kruemmungsvektor p''(t) kann in einen Anteil innerhalb der Tangentialebene und in einen senkrecht dazu zerlegt werden. Den Betrag des ersteren nennt man geodaetische Kruemmung kg(t), den des letzteren die Normalkruemmung kn(t). Kurven mit verschwindender geodaetischer Kruemmung (wie zum Beispiel die Grosskreise auf einer Sphaere) heissen Geodaeten. Sie sind das Analogon von Parallelen in der Ebene.
Wenn man alle moeglichen Flaechenkurven variiert, die durch einen bestimmten Flaechenpunkt hindurchgehen, variiert die Normalkruemmung mit. Die Richtungen, in denen die Normalkruemmung ihr Maximum k1 bzw Minimum k2 annimmt, heissen Hauptkruemmungsrichtungen der Flaeche im Punkt f(t1,t2). Es gilt: k1*k2=(L11*L22-L12**2)/(g11*g22-g12**2) und: k1+k2=(L22*g11-2*L12*g12+L11*g22)/(g11*g22-g12**2), wobei Lij=n(t1,t2).d^2f(t1,t2)/dt1/dt2 und n der Normalenvektor im Punkt f(t1,t2) ist.
Die Summe (k1+k2)/2 heisst mittlere Kruemmung H und das Produkt k1*k2 heisst Gauss'sche Kruemmung K. Beide sind unabhaengig von der Parametrisierung der Flaeche durch Parameter t1,t2. Nach dem Theorema Egregium von Gauss kann die Gauss'sche Kruemmung darueberhinaus allein durch die Metrik gij und ihre Ableitungen ausgedrueckt werden.
In einem gekruemmten Dreieck, wie es Gauss vermessen hat, ist der Winkeldefekt alpha+beta+gamma-pi proportional zum Integral der Gauss'schen Kruemmung ueber die Dreiecksflaeche. Im Fall einer Sphaere reduziert sich dieses Theorem auf alpha+beta+gamma-pi=Dreiecksflaeche/r**2, wobei r der Radius der Sphaere ist. Wenn, wie bei Gauss' Messungen, Dreiecksflaeche und Winkeldefekt bekannt sind, kann man daraus r bestimmen.
3. Kruemmung eines Lichtstrahls im Gravitationsfeld der Erde
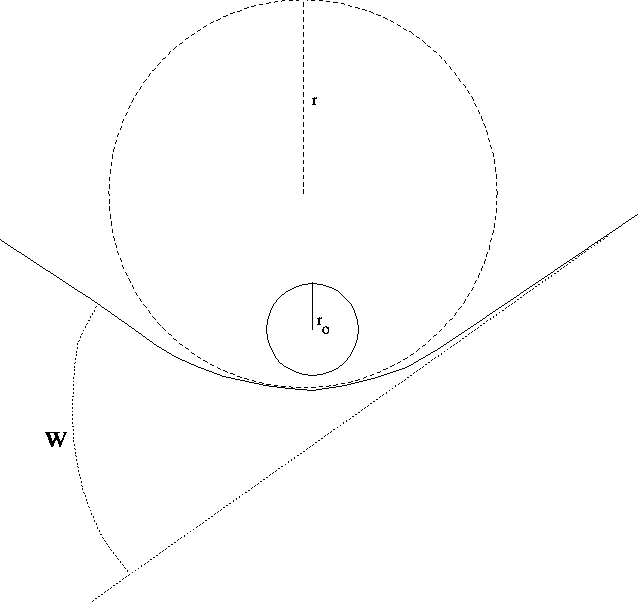
Ein Lichtstrahl, der sich ueber der Erdoberflaeche bewegt, wird durch verschiedene Effekte von seiner geraden Bahn abgelenkt, zum Beispiel durch die Brechung des Lichtes in der Erdathmosphaere, aber auch durch das Gravitationsfeld der Erde. Letzteres ist - in sehr uebertriebener Weise in der beigefuegten Figur skizziert. Darin ist r0 der Radius der Erde und r der Radius des asymptotischen Kreises, den man an den gekruemmten Lichtstrahl zeichnen kann. W ist der Winkel, um den der Lichtstrahl abgelenkt wird. Man kann ihn nach der allgemeinen Relativitaetstheorie ausrechnen und erhaelt einen Wert von etwa 10**(-8) Grad. Dazu gehoert ein Kreisradius von r=10**10 Metern. Fuer das von Gauss bei seiner (fiktiven) Messung benutzte Dreieck zwischen Harz, Rhoen und rheinischem Bergland, das sich ja nur ueber einen kleinen Teil der Erdkugel erstreckt, ergibt sich daraus ein Winkeldefekt von grob 10**(-10) Grad. Diese Genauigkeit haette er erreichen muessen, um den Effekt tatsaechlich nachzuweisen.
4. Die hyperbolische Ebene
Das ist die Ebene, die von Punkten (z,t) mit der Metrik (d.h. Definition des Abstandes d zum Nullpunkt) d**2=t**2-z**2 gebildet wird. Sie ist eindeutig festgelegt, wenn man eine konstante negative Gauss'sche Kruemmung voraussetzt. Durch Wahl geeigneter Koordinaten kann man dort immer K=-1 erreichen. Zum Vergleich: die euklidische Ebene hat K=0 und die Sphaere hat ebenfalls eine konstante Gauss'sche Kruemmung, jedoch positiv K>0. Bei der Sphaere kann man durch Einfuehrung geeigneter Koordinaten immer K=1 erreichen. Es gibt uebrigens auch in der euklidischen Geometrie die Moeglickeit, in einem kleinen Teilgebiet einer Flaeche negative Gauss'sche Kruemmung K<0 zu haben (jedoch nicht ueber die gesamte Flaeche hinweg), und zwar auf Sattelflaechen.
Die euklidische Ebene erfuellt das euklidische Parallelenaxiom: Zu einem gegebenen Punkt und einer gegebenen Geraden gibt es nicht mehr als eine Gerade durch den gegebenen Punkt, die zu der gegebenen Gerade parallel ist.
Die hyperbolische Ebene erfuellt das hyperbolische Parallelenaxiom: Zu einem gegebenen Punkt und einer gegebenen Gerade gibt es mehr als eine Gerade durch den gegebenen Punkt, die zu der gegebenen Gerade parallel ist.
Die Gleichungen der hyperbolischen Geometrie ergeben sich, indem man in den Formeln der euklidischen Geometrie ueberall sinus und cosinus durch sinus hyperbolicus und cosinus hyperbolicus ersetzt. Dieser Uebergang macht zum Beispiel aus gewoehnlichen, euklidischen Rotationen Lorentztransformationen, also Drehungen zwischen Raum- und Zeit-koordinaten.
5. Die Taetigkeit des Geometers
Grundlage der Geodaesie war frueher (und ist teilweise heute noch) die Triangulation. Dabei wird ein Landstrich in kleinere und groessere Dreiecke unterteilt, und man beginnt die Messungen mit den kleinen, absolut praezise vermessenen Triangeln, um danach zu groesseren ueberzugehen, die mit den kleinen einen gemeinsamenen Schenkel haben.
Das wichtigste Instrument der Vermessungskunde war der Theodolit, der zur Bestimmung von horizontalen und vertikalen Winkeln benutzt werden kann. Er besteht hauptsaechlich aus einem Fernrohr mit Fadenkreuz und kann um zwei Achsen in jede raeumliche Richtung gedreht werden. Die Stellwinkel sind mit einem Nonius auf zwei Teilkreisen genau bestimmbar und eine exakt waagerechte Justierung erreicht man mit Hilfe von Libellen.
Gauss Weiterentwicklung des Theodolithen ist zusammen mit ihm selbst auf dem letzten 10 Mark Schein der Bundesrepublik Deutschland abgebildet.
6. Der fiktive Gauss
Zeittafel:
| 1777 | Geburt in Braunschweig |
| 1795 | Beweis der Konstruierbarkeit des regelmaessigen 17-Ecks |
| 1796 | Studium in Goettingen |
| 1799 | Rueckkehr nach Braunschweig |
| 1803 | Gauss lernt Hanna kennen, Heirat |
| 1807 | Direktor der Sternwarte Goettingen |
| 1810 | Gauss lernt Wilhelm Weber kennen |
| 1813 | Tod von Hanna Gauss |
| 1817 | Gauss' Ende |
7. Der reale Gauss
Die meisten Teile der Novelle sind frei erfunden. Der reale Gauss war eine wesentlich robustere Natur als der imaginaere. Er hat seine Hanna, mit der er uebrigens zwei Kinder hatte, zwar durch fruehen Tod verloren und darunter unsaeglich gelitten, das hielt ihn aber nicht davon ab, keine 5 Monate spaeter um die zweite Ehefrau anzuhalten, mit der er noch einmal drei Kinder zeugte. Er war - nicht nur als Wissenschaftler - ein Pragmatiker, der sich selten romantischen Stimmungen ueberliess. Die zweite Ehe ist uebrigens wesentlich weniger gluecklich gewesen als die erste, und mit den beiden Soehnen aus dieser Verbindung hat Gauss sich ueberhaupt nicht verstanden.
Der reale Gauss hat zwar die Konstruierbarkeit des regulaeren 17-Eck bewiesen, zur Entdeckung der Ceres beigetragen und Geometrie und Zahlentheorie wie keiner vor oder nach ihm befruchtet, er hat auch die Theorie der Flaechenkruemmung soweit entwickelt, dass es Riemann und Einstein nicht schwerfiel, sie auf hoeherdimensionale Strukturen zu verallgemeinern, doch der physikalische Nachweis der Konstanz der Lichtgeschwindigkeit in allen Inertialsystemen beziehungsweise der Kruemmung von Lichtstrahlen im Gravitationsfeld der Erde, die die Voraussetzung fuer die spezielle beziehungsweise die allgemeine Relativitaetstheorie sind, haette ihm niemals gelingen koennen. Die damals bei geodaetischen Messungen erreichte Genauigkeit lag um viele Zehnerpotenzen zu niedrig. Dass er solche Messungen im Harz vorhatte, wird unter seinen Bewunderern noch heute oft kolportiert.
Aus dramaturgischen Gruenden habe ich die Rolle des Genies Gauss uebertrieben. In Wahrheit ist der Einzelne, ob er nun Gauss oder Einstein heisst, wenig im Vergleich zu der kollektiven Anstrengung, die man Wissenschaft nennt.
Der reale Gauss hatte zwar einen treuen Mitarbeiter und Knecht Weber, und einen Astronomen Harding, den er sich zum Feind machte, nachdem er dessen Vorgesetzter wurde, es gab aber keinen ausgepraegten Widerpart Haeussler und es ist nicht bekannt, dass er jemals einem Menschen dermassen geschadet haette, wiewohl er - besonders in der zweiten Lebenshaelfte (Gauss ist 78 Jahre alt geworden) - im persoenlichen Umgang launisch, ja boesartig sein konnte.
Copyright: B. Lampe, 1998
e-mail: Lampe.Bodo@web.de